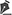CENÁRIO PRÁTICO A chefe de uma UTI gostaria de avaliar se pacientes obesos admitidos por exacerbação de DPOC têm um tempo de permanência (TdP) hospitalar mais longo do que pacientes não obesos. Depois de recrutar 200 pacientes, ela descobriu que a distribuição do TdP é fortemente inclinada para a direita (Figura 1A). Se ela fizesse um teste de hipótese, seria apropriado usar um teste t para comparar o TdP de pacientes obesos e não obesos com exacerbação de DPOC?
TESTES PARAMÉTRICOS VS. TESTES NÃO PARAMÉTRICOS EM ESTATÍSTICA Testes paramétricos assumem que a distribuição dos dados é normal ou em forma de sino (Figura 1B) para testar as hipóteses. Por exemplo, o teste t é um teste paramétrico que assume que o desfecho de interesse tem uma distribuição normal, que pode ser caracterizada por dois parâmetros
(1): a média e o desvio-padrão (Figura 1B).
Testes não paramétricos não exigem que os dados cumpram essa suposição de distribuição restritiva para a variável de desfecho. Portanto, eles são mais flexíveis e podem ser amplamente aplicados a várias distribuições diferentes. As técnicas não paramétricas usam rank
(1) ao invés dos valores reais das observações. Por esse motivo, além de dados contínuos, podem ser usadas para analisar dados ordinais, para os quais os testes paramétricos costumam ser inadequados.
(2) Quais são as armadilhas? Se a variável de desfecho for normalmente distribuída e as exigências para o uso de testes paramétricos forem atendidas, as técnicas não paramétricas têm menor poder estatístico do que os testes paramétricos comparáveis.
Isso significa que os testes não paramétricos têm menos probabilidade de detectar um resultado estatisticamente significativo (ou seja, menos probabilidade de encontrar um valor p < 0,05 do que um teste paramétrico). Além disso, os testes paramétricos fornecem estimativas de parâmetros — no caso do teste t, a média e o desvio-padrão são os parâmetros calculados — e um intervalo de confiança para esses parâmetros. Por exemplo, em nosso cenário prático, se a diferença no TdP entre os grupos fosse analisada com um teste t, iríamos obter a diferença média amostral no TdP entre os grupos e o desvio-padrão dessa diferença no TdP. Finalmente, o intervalo de confiança de 95% da diferença média amostral poderia ser relatado para expressar a faixa de variação para a diferença média na população. Por outro lado, os testes não paramétricos não estimam parâmetros, como média, desvio-padrão ou intervalos de confiança. Eles calculam apenas um valor de p.
(2) COMO ESCOLHER ENTRE TESTES PARAMÉTRICOS E NÃO PARAMÉTRICOS? Quando o tamanho da amostra é grande, ou seja, superior a 100, testes paramétricos geralmente podem ser aplicados independentemente da distribuição da variável de desfecho. Isso se deve ao teorema do limite central, que afirma que, se o tamanho da amostra for grande o suficiente, a distribuição de uma determinada variável é aproximadamente normal. Quanto mais a distribuição se afasta da normalidade, maior será o tamanho da amostra necessário para se aproximar da normalidade.
Quando o tamanho da amostra é pequeno e a distribuição da variável de desfecho é extremamente não normal, os testes não paramétricos são mais apropriados. Por exemplo, algumas variáveis são naturalmente assimétricas, como tempo de internação ou número de exacerbações de asma por ano. Nesses casos, variáveis extremamente assimétricas devem sempre ser analisadas com testes não paramétricos, mesmo com grandes tamanhos amostrais.
(2) Em nosso cenário prático, como a distribuição de TdP está fortemente desviada para a direita, a relação entre obesidade e TdP em pacientes hospitalizados por exacerbações de DPOC deve ser analisada com um teste não paramétrico (teste da soma de ranks de Wilcoxon ou teste de Mann-Whitney) em vez de um teste t.
REFERÊNCIAS
- Whitley E, Ball J. Statistics review 6: Nonparametric methods. Crit Care. 2002;6(6):509-513. https://doi.org/10.1186/cc1820
- e Cessie S, Goeman JJ, Dekkers OM. Who is afraid of non-normal data? Choosing between parametric and non-parametric tests. Eur J Endocrinol. 2020;182(2):E1-E3. https://doi.org/10.1530/EJE-19-0922