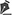PRACTICAL SCENARIO
 
The head of an ICU would like to assess if obese patients admitted for a COPD exacerbation have a longer hospital length of stay (LOS) than do non-obese patients. After recruiting 200 patients, she finds that the distribution of LOS is strongly skewed to the right (Figure 1A). If she were to perform a test of hypothesis, would it be appropriate to use a t-test to compare LOS between obese and non-obese patients with a COPD exacerbation?

 
PARAMETRIC VS. NONPARAMETRIC TESTS IN STATISTICS
 
Parametric tests assume that the distribution of data is normal or bell-shaped (Figure 1B) to test hypotheses. For example, the t-test is a parametric test that assumes that the outcome of interest has a normal distribution, that can be characterized by two parameters(1): the mean and the standard deviation (Figure 1B).
 
Nonparametric tests do not require that the data fulfill this restrictive distribution assumption for the outcome variable. Therefore, they are more flexible and can be widely applied to various different distributions. Nonparametric techniques use ranks(1) instead of the actual values of the observations. For this reason, in addition to continuous data, they can be used to analyze ordinal data, for which parametric tests are usually inappropriate.(2)
 
What are the pitfalls? If the outcome variable is normally distributed and the assumptions for using parametric tests are met, nonparametric techniques have lower statistical power than do the comparable parametric tests. This means that nonparametric tests are less likely to detect a statistically significant result (i.e., less likely to find a p-value < 0.05 than a parametric test). Additionally, parametric tests provide parameter estimations—in the case of the t test, the mean and the standard deviation are the calculated parameters—and a confidence interval for these parameters. For example, in our practical scenario, if the difference in LOS between the groups were analyzed with a t-test, it would report a sample mean difference in LOS between the groups and the standard deviation of that difference in LOS. Finally, the 95% confidence interval of the sample mean difference could be reported to express the range of values for the mean difference in the population. Conversely, nonparametric tests do not estimate parameters such as mean, standard deviation, or confidence intervals. They only calculate a p-value.(2)
 
HOW TO CHOOSE BETWEEN PARAMETRIC AND NONPARAMETRIC TESTS?
 
When sample sizes are large, that is, greater than 100, parametric tests can usually be applied regardless of the outcome variable distribution. This is due to the central limit theorem, which states that if the sample size is large enough, the distribution of a given variable is approximately normal. The farther the distribution departs from being normal, the larger the sample size will be necessary to approximate normality.
 
When sample sizes are small, and outcome variable distributions are extremely non-normal, nonparametric tests are more appropriate. For example, some variables are naturally skewed, such as hospital LOS or number of asthma exacerbations per year. In these cases, extremely skewed variables should always be analyzed with nonparametric tests, even with large sample sizes.(2)
 
In our practical scenario, because the distribution of LOS is strongly skewed to the right, the relationship between obesity and LOS among the patients hospitalized for COPD exacerbations should be analyzed with a nonparametric test (Wilcoxon rank sum test or Mann-Whitney test) instead of a t-test.
 

1. Whitley E, Ball J. Statistics review 6: Nonparametric methods. Crit Care. 2002;6(6):509-513. https://doi.org/10.1186/cc1820


2. e Cessie S, Goeman JJ, Dekkers OM. Who is afraid of non-normal data? Choosing between parametric and non-parametric tests. Eur J Endocrinol. 2020;182(2):E1-E3. https://doi.org/10.1530/EJE-19-0922