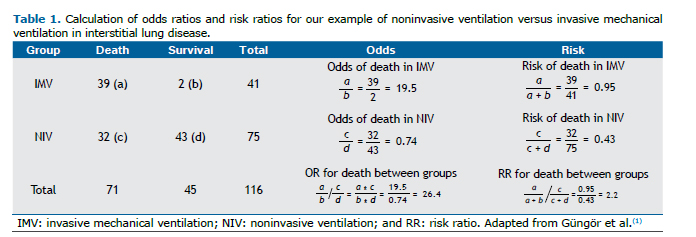
PRACTICAL SCENARIOA retrospective cohort study evaluated the association between type of ventilatory support and mortality among adult patients with interstitial lung disease and acute respiratory failure.(1) In comparison with noninvasive ventilation (NIV), invasive mechanical ventilation (IMV) increased mortality, with an OR of 26.0 (95% CI: 5.9-116.6) and a risk ratio (RR) of 2.2 (95% CI: 1.7-2.9), as detailed in table 1.
In our example, we calculated the OR and RR to answer the study question. It is important to understand the difference between these two statistical methods for calculating risk, which one is more applicable to answer this research question, and how they are interpreted.
The OR is defined as the ratio of odds of an event occurring, estimated by calculating the ratio of the number of times that the event of interest occurs to the number of times that it does not (ratio of events to non-events) between exposed and unexposed groups.(2) The RR is defined as the ratio of probabilities of an event occurring (ratio of events to subjects) between exposed and unexposed groups (Table 1). A positive association (increased risk) between exposure and outcome implies that the OR or RR is > 1.0, and a negative association (decreased risk) implies that the OR or RR is < 1.0.
HOW THE RR AND OR SHOULD BE INTERPRETEDThe RR expresses that the "risk of the event (e.g., mortality) is X times larger/smaller in the exposed group than in the unexposed group". That statement is easily interpreted because it deals with probabilities (which range from 0 to 1). However, the OR is expressed as the ratio of the odds of event X in the exposed group to the odds of the same event in the unexposed group. Although we often use ORs to estimate RRs, they are different and ORs are not as intuitive to grasp and are therefore often misinterpreted.
The RR is commonly (and most correctly) used in order to estimate the risk of an event in randomized controlled trials, cohort studies, and cross-sectional studies, because all of those study designs calculate absolute risk and the RR can therefore be estimated. The OR is utilized to estimate risk in case-control studies, where the prevalence/incidence of the outcome cannot be estimated, given that the numbers of individuals with and without the outcome (cases and controls, respectively) are fixed by the investigators. The OR is also commonly used in order to calculate risk in cohort studies and randomized controlled trials when a logistic regression statistical model is employed to adjust for confounders or test for effect modification. However, we should bear in mind the fact that ORs and RRs are not equivalent.
In comparison with an RR, an OR tends to overestimate the strength of the association between exposure and outcome. However, the degree of overestimation is negligible in studies in which the outcome of interest occurs rarely (typically in < 10% of the participants). In our example, the ratio of the odds of death in the IMV group to that in the NIV group is 26 to 1 (OR = 26.0). In contrast, the risk of death in patients on IMV is 95%, compared with 43% for those on NIV (RR = 2.2). That RR is interpreted as the risk of death being 2.2 times higher in the IMV group than in the NIV group. This large difference between OR and RR is explained by the high proportion of participants who died in our example (41%). The OR estimates the RR more accurately when the study outcome is rare.
REFERENCESGüngör G, Tatar D, Saltürk C, Çimen P, Karakurt Z, Kirakli C, et al. Why do patients with interstitial lung diseases fail in the ICU? a 2-center cohort study. Respir Care. 2013;58(3):525-531. https://doi.org/10.4187/respcare.01734
Sistrom CL, Garvan CW. Proportions, odds, and risk. Radiology. 2004;230(1):12-19. https://doi.org/10.1148/radiol.2301031028